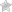Формула циклической частоты свободных колебаний пружинного маятника

Таким образом, полная энергия гармонического колебания
постоянна и пропорциональна квадрату амплитуды смещения. Это – одно из
характерных свойств гармонических колебаний. Здесь постоянный коэффициент k в
случае пружинного маятника означает жёсткость пружины, а для математического
маятника k=mgH. В обоих случаях коэффициент k передаётся параметрами
колебательной системы.

Полная энергия механической колебательной системы
состоит из кинетической и потенциальной энергий и равна максимальному значению
любой из этих двух составляющих:

Следовательно, полная энергия колебаний прямо
пропорциональна квадрату амплитуды смещения или квадрату амплитуды скорости.

Из
формулы:

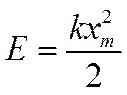
• можно определить амплитуду xm колебаний смещения:

•  

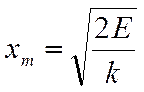
• Амплитуда смещения при свободных колебаниях прямо
  пропорциональна корню квадратному из энергии, сообщённой колебательной системе
  в начальный момент, когда систему выводили из состояния равновесия.

1.  Кинематика механических свободных колебаний
2.      1      Смещение,
   скорость, ускорение. Для нахождения кинематических характеристик (смещения,
   скорости и ускорения) свободных колебаний воспользуемся законом сохранения и
   превращения энергии, которой для идеальной механической колебательной системы
   записывается так:

3.  

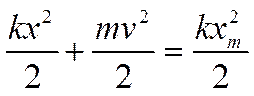
4. или

5.  

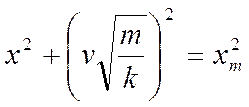
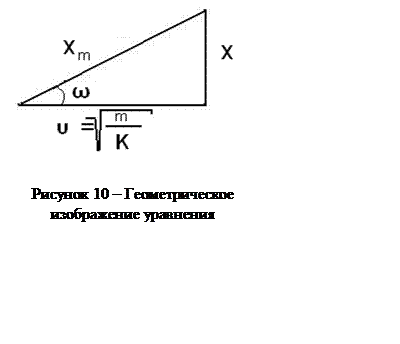
Полученное равенство можно представить геометрически в
виде прямоугольного треугольника, у которого xm –
гипотенуза, а x и v —
катеты ( рис. 10). Из рисунка видно, что

 

 

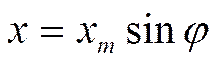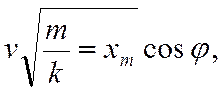
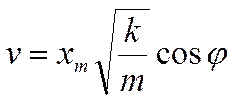          Из
второго равенства находим выражение для мгновенной скорости, так как при
колебании системы смещение x непрерывно изменяется, а амплитуда колебаний xm является постоянной величиной, то непрерывно изменяется и угол.
Выясним, как изменяется этот угол φ.

• Для
  этого выразим скорость v как производную от смещения x по времени t:
• υ= x' = xm
  cosφ · φ'
• Приравняв полученные два
  выражения для скорости, получим:

•  

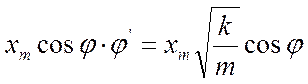
• или
•  
• Обозначим эту постоянную
  величину через ω0:
•  
• Так как производная по времени φ'
  постоянна, то угол φ зависит от времени линейно:
• φ=ω0t
• Учитывая
  это можно записать:
• x = xm sin ω0t, υ = xm ω0 cos ω0t
• Здесь величина
• xmω0 = υm
• есть амплитуда изменения
  скорости:
• υ = υm cos ω0t
• Зависимость мгновенного значения ускорения a
  от времени t мы найдём как производную скорости υ по времени:
• a = υ' = — ω0υm
  sin ω0t,
• или
• a = -am sin ω0t
• знак
  «-» в полученной формуле указывает на то, что знак проекции вектора ускорения
  на ось, вдоль которой происходят колебания, противоположен знаку смещения x.
• Итак,
  мы видим, что при гармонических колебаниях не только смещение, но и скорость и
  ускорение изменяются синусоидально.

     2
Циклическая частота колебаний.Величина ω0 называется
циклической частотой колебаний. Так как функция sin α
имеет по аргументу α  период 2π, а гармонические колебания имеют по времени
период T, то

1. ω0T = 2π
2. Отсюда
3.  
4. или
5. Так
   как частота υ выражает число колебаний за 1 с, то циклическая частота ω
   выражает число колебаний за 2π с.
6.      3      Формулы частоты и периода свободных
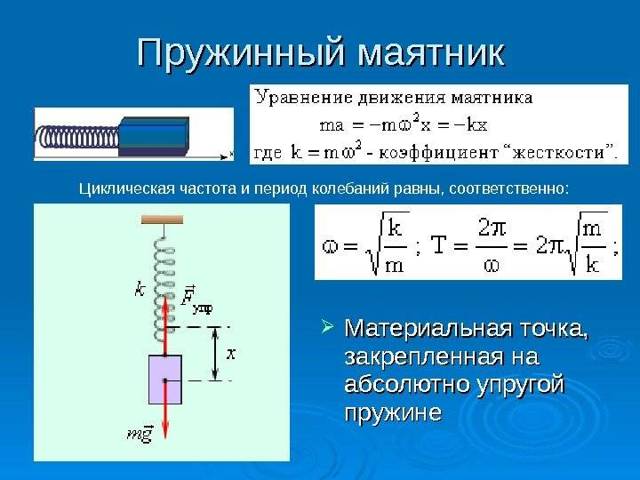
   колебаний для пружинного и математического маятников.Формула
   циклической частоты
7. непосредственно
   применима для вычисления циклической частоты свободных колебаний пружинного
   маятника (k -жёсткость пружин).
8. Чтобы получить формулу циклической частоты свободных
   колебаний пружинного маятника, надо вместо k подставить l.
   Тогда получим:
9. Так
   как
10.  
11. то для периода свободных
    колебаний имеем:
12. — в случае пружинного
    маятника
13. и
14.           — в случае
    математического маятника.

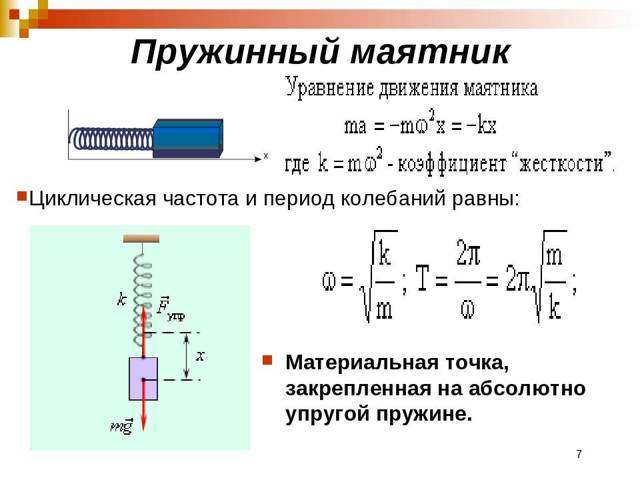
Пружинный маятник: период и амплитуда колебани1, формула, жесткость

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.

Приняты следующие обозначения:

• m — масса тела;
• k — коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

• Сочетание тела и пружины.Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;
• У любой пружины есть исходное положение, предел сжатия и растяжения.При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;
• Полная механическая энергия появляется с началом процесса обратимого деформирования.В этот момент на объект не оказывает действие сила упругости;
• Колебательные движения происходят под влиянием силы упругости.Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;
• От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения.Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Свободные колебания

Уравнение вида x ¨ + ω 0 2 x = 0 получило название уравнения свободных колебаний. Их физические свойства могут определять только собственную частоту колебаний ω 0 или период Т .

Амплитуда x m и начальная фаза φ 0 находят при помощи способа, который вывел их из состояния равновесия начального момента времени.

При наличии смещенного груза из положения равновесия на расстояние ∆ l и моменте времени, равном t = 0 , производится его опускание без начальной скорости. Тогда x m = ∆ l , φ 0 = 0 . Если груз находился в положении равновесия, то при толчке передается начальная скорость ± υ 0 , отсюда x m = m k υ 0 , φ 0 = ± π 2 .

Амплитуда x m с начальной фазой φ 0 определяются наличием начальных условий.

Рисунок 2 . 2 . 2 . Модель свободных колебаний груза на пружине.

Механические колебательные системы отличаются наличием сил упругих деформаций в каждой из них. Рисунок 2 . 2 . 2 показывает угловой аналог гармонического осциллятора, совершающий крутильные колебания. Диск располагается горизонтально и висит на упругой нити, закрепленной в его центре масс. Если его повернуть на угол θ , тогда возникает момент силы упругой деформации кручения M у п р :

Данное выражение не соответствует закону Гука для деформации кручения. Величина x аналогична k жесткости пружины. Запись второго закона Ньютона для вращательного движения диска принимает вид

• I ε = M у п р = — x θ или I θ ¨ = — x θ , где моментом инерции обозначается I = I C , а ε – угловое ускорение.
• Аналогично с формулой пружинного маятника:
• ω 0 = x I , T = 2 π I x .

Применение крутильного маятника замечено в механических часах. Он получил название балансира, в котором создание момента упругих сил производится при помощи спиралевидной пружины.

Рисунок 2 . 2 . 3 . Крутильный маятник.

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​(
  u )​ < 16 Гц);
• звуковой диапазон (16 Гц < ( u ) < 20 000 Гц);
• ультразвук ((
  u ) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

1. Скорость звука зависит
2. от упругих свойств среды:
3. в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
4. от температуры среды:
5. в воздухе при температуре 0°С – 331 м/с, в воздухе при температуре +15°С – 340 м/с.
6. Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.Шум – хаотическая смесь тонов.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника. 

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик).

При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения.

Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Формула для расчета периода колебаний пружинного маятника

• Механика (56)
  • Кинематика (19)
  • Динамика и статика (32)
  • Гидростатика (5)
• Молекулярная физика (25)
  • Уравнение состояния (3)
  • Термодинамика (15)
  • Броуновское движение (6)
  • Прочие формулы по молекулярной физике (1)
• Колебания и волны (22)
• Оптика (9)
  • Геометрическая оптика (3)
  • Физическая оптика (5)
  • Волновая оптика (1)
• Электричество (39)
• Атомная физика (15)
• Ядерная физика (3)

• Квадратный корень, рациональные переходы (1)
• Квадратный трехчлен (1)
• Координатный метод в стереометрии (1)
• Логарифмы (1)
• Логарифмы, рациональные переходы (1)
• Модуль (1)
• Модуль, рациональные переходы (1)
• Планиметрия (1)
• Прогрессии (1)
• Производная функции (1)
• Степени и корни (1)
• Стереометрия (1)
• Тригонометрия (1)
• Формулы сокращенного умножения (1)

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng! Занимаюсь там сам — очень круто. Прогресс налицо.

https://www.youtube.com/watch?v=Vh9q03WXM7I\u0026t=640s

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке! Жмите СЮДА

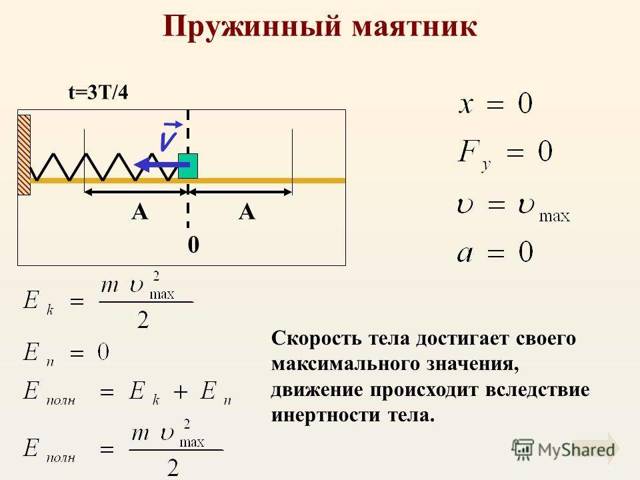
Период пружинного маятника — зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается

Пружинный маятник — это груз, колеблющийся на пружине. Он совершает возвратно-поступательное движение. Пружинный маятник подчиняется законам движения, по которым можно определить период его колебаний, зная массу груза и жесткость пружины. Период колебаний пружинного маятника не зависит от места его расположения и амплитуды колебаний.

• Давайте выведем формулу периода пружинного маятника.
• На груз m горизонтального пружинного маятника действуют сила тяжести (mg), сила реакции опоры (N) и сила упругости пружины (Fynp). Запишем второй закон Ньютона для данного случая :
• Все проецируем на ось ОХ:
• Запишем это уравнение в форме аналогичной уравнению движения гармонического осциллятора:
• Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:
• Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:
• Тогда период колебаний пружинного маятника будет равен:

• Период физического маятника
• Период крутильного маятника
• В Формуле мы использовали :
• — Период пружинного маятника маятника
• — Масса груза
• — Изменение длины пружины
• — Коэффициент упругости пружины
• — Ускорение свободного падения
• — Циклическая частота пружинного маятника
• — Сила реакции опоры
• — Сила упругости

Формула периода колебаний пружинного маятника

1. Период — это минимальное время, за которое совершается одно полное колебательное движение.
2. Обозначают период буквой $T$.
3. где $Delta t$ — время колебаний; $N$ — число полных колебаний.

Уравнение колебаний пружинного маятника

Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k $(рис.1).

Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести.

Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:

• Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
• Ускорение груза запишем, помня, что движение происходит по оси X, как:
• Второй закон Ньютона для груза принимает вид:
• Учтем равенство (2), формулу (5) преобразуем к виду:
• Если ввести обозначение: $^2_0=frac$, то уравнение колебаний запишем как:
• где $^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
• где $_0=sqrt>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

Связь между внутренней энергией тела кинетической и потенциальной энергиями

Между кинетической и потенциальными понятиями есть определенная взаимосвязь. Для расчета подобной связи используется следующая формула: А=Fs=mav 2 2-v 2 1/2a.

Оба значения применяются в качестве полезного действия, могут варьировать в достаточно большом диапазоне, а также зависеть от различных факторов.

В заключение отметим, что проводимые расчеты позволяют выбрать наиболее подходящий вариант исполнения изделия для конкретного механизма. При исследовании проводится отображение схемы, на которой можно увидеть распространение всех сил.

Механические колебания | Механика | Теория | Решутест. Продвинутый тренажёр тестов

Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.

Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.

Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac{1}{T}$ , где

• v ― частота [Гц];
• T ― период [c].
• Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac{N}{t}$ , где
• ν ― частота [Гц];
• N ― количество колебаний;
• t - время [с].
• Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac{2pi}{T}$ , где
• ω ― циклическая частота [рад/с];
• ν ― частота [Гц];
• T ― период [c].
• Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
• x(t) = Asin(ωt + φ0) или x(t) = Acos(ωt + φ0), где
• x ― смещение [м];
• t ― время, [с];
• A ― амплитуда колебаний [м];
• ω ― циклическая частота [рад/с];
• φ0 ― начальная фаза колебаний, [рад];
• (ωt + φ0) ― полная фаза колебаний [рад].

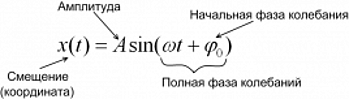
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.

Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.

1. Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
2. Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
3. φ ― полная фаза колебаний [рад];
4. φ0 ― начальная фаза колебаний, [рад];
5. ω ― циклическая частота [рад/с];
6. t ― время, [с].
7. Пример анализа гармонических колебаний точки
8. Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
9. x ― смещение [м];
10. t ― время, [с];
11. A — амплитуда колебаний [м];
12. ω ― циклическая частота [рад/с].

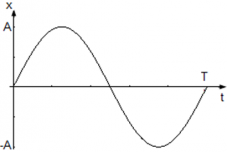
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия.

Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1.

Когда x = A фаза колебаний равна φ = $frac{pi}{2} +2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac{3pi}{2} +2pi n$ , где n = 0, 1 , 2, … N.

График колебания координаты точки имеет вид:

• Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt', где
• v ― скорость движения точки [м/с];
• x ― координата точки [м];
• t ― время, [с].
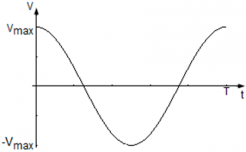
• Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt' = |Asin(ωt)|'t = Acos(ωt).
• Уравнение скорости точки равно v(t) = Acos(ωt), где
• v ― скорость движения точки [м/с];
• A — амплитуда колебаний [м];
• ω ― циклическая частота [рад/с];
• t ― время, [с].

Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.

График колебания скорости точки имеет вид:

1. Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
2. Ускорение ― это производная скорости по времени: a = vt', где
3. a ― ускорение движения точки [м/с2];
4. v ― скорость движения точки [м/с];
5. t ― время, [с].
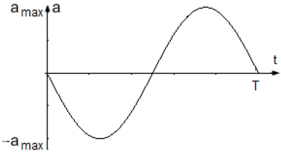
6. Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt' = [Aωcos(ωt)]t' = –Aω2sin(ωt).
7. Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
8. a ― ускорение движения точки [м/с2];
9. A — амплитуда колебаний [м];
10. ω ― циклическая частота [рад/с];
11. t ― время, [с].

Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.

График колебания ускорения точки имеет вид:

Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации.

В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную.

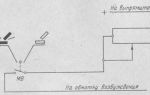
Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где

• E ― полная механическая энергия системы, E = const, [Дж];
• EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
• EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
• Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).

1. Потенциальная энергия деформированной пружины равна EП = $frac{kx^2}{2}$ , где
2. EП ― потенциальная энергия деформированной пружины, [Дж];
3. k ― коэффициент упругости пружины [Н/м];
4. x ― деформация пружины (величина ее удлинения или сжатия) [м].

У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac{k(x(t))^2}{2}$ = $frac{k(Asin(omega t))^2}{2}$ = $frac{k}{2} cdot A^2 sin^2 (omega t)$ .

• Уравнение потенциальной энергии пружинного маятника EП = $frac{k}{2} cdot A^2 sin^2 (omega t)$ , где
• EП ― потенциальная энергия пружинного маятника, [Дж];
• k ― коэффициент упругости пружины [Н/м];
• A — амплитуда колебаний [м];
• ω ― циклическая частота [рад/с];
• t ― время, [с].
• Амплитуда потенциальной энергии пружинного маятника равна EПmax = $frac{k}{2}A^2$ , где
• EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
• k ― коэффициент упругости пружины [Н/м];
• A — амплитуда колебаний [м].

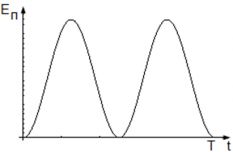
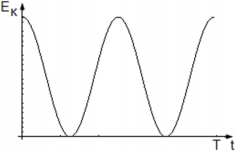
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.

График колебаний потенциальной энергии пружинного маятника:

1. Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac{mv^2}{2}$ , где
2. Eк ― кинетическая энергия тела, [Дж];
3. m ― масса тела, [кг];
4. v ― скорость движения тела, [м/с].
5. У тела, которое совершает колебательные движения, скорость ― переменная величина.

Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac{m(v(t))^2}{2}$ = $frac{m}{2} cdot (Aomegacos(omega t))^2$ = $frac{m}{2} cdot A^2 omega^2 cos^2 (omega t)$ .

• Уравнение кинетической энергии маятника Eк = $frac{m}{2} cdot A^2 omega^2 cos^2 (omega t)$ , где
• Eк ― кинетическая энергия маятника, [Дж];
• m ― масса тела, [кг];
• A — амплитуда колебаний [м];
• ω ― циклическая частота [рад/с];
• t ― время, [с].
• Амплитуда кинетической энергии маятника равна EКmax = $frac{m}{2} cdot A^2 omega^2$ , где
• EКmax ― максимальная кинетическая энергия маятника, [Дж];
• m ― масса тела, [кг];
• A — амплитуда колебаний [м];
• ω ― циклическая частота [рад/с].
• Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
• График колебаний кинетической энергии маятника:

1. Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
2. Период колебаний математического маятника равен T = $2pi sqrt{frac{l}{g}}$ , где
3. T ― период колебаний [с];
4. l ― длина нити математического маятника [м];
5. g ― ускорение свободного падения [м/с2].
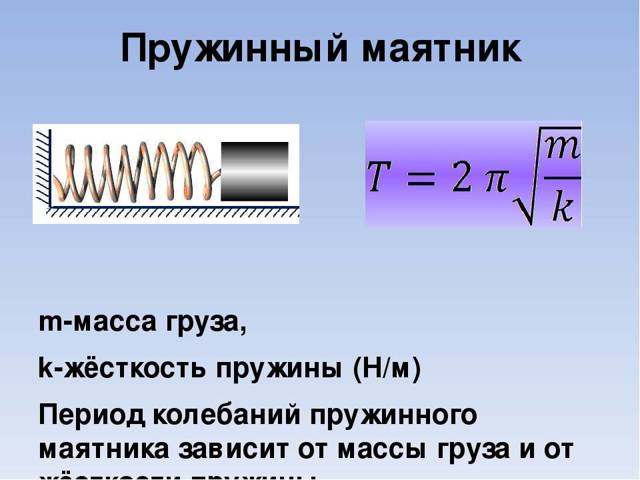
6. Период колебаний пружинного маятника равен T = $2pi sqrt{frac{m}{k}}$ , где
7. T ― период колебаний [с];
8. m ― масса груза [кг];
9. k ― жесткость пружины [Н/м].

Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.

Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.

На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.

Формула циклической частоты свободных колебаний пружинного маятника — Мастерок

• Маятник на пружине — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
• Период колебаний пружинного маятника может быть вычислен по следующей формуле:
• T = 2 π m k .

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения. Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

1. В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.
2. Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
3. m a = − k x ⟺ x ¨ + k m x = 0
4. Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
5. x ¨ + k m x = f ( x ) , где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.
6. В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
7. x ¨ + c m x ˙ + k m x = f ( x )

Свойства пружинного маятника

Идеальный пружинный маятник представляет собой пружину, массой которой можно пренебречь, с закрепленным на ней телом с точечной массой. При этом один или оба конца пружины закреплены, а силой трения можно пренебречь.

Такую конструкцию можно рассматривать лишь как математическую модель. Примерами реальных пружинных маятников (навитых из упругой проволоки цилиндрических спиралей) могут служить всевозможные устройства, гасящие колебания: амортизаторы, подвески, рессоры и т.п. Пружинные маятники, хотя и несколько иной конструкции (в виде плоских спиралей) используются в механических часах.

Читать также:  Влажное бритье электробритвой как это

Свойства пружин зависят от вещества, из которого они изготовлены (как правило, это особая пружинная сталь), диаметра проволоки, формы ее сечения, диаметра цилиндра пружины, его длины. Эти показатели в совокупности обуславливают ключевую характеристику пружины – ее жесткость.

Пружина запасает энергию при продольном растяжении или сжатии за счет упругих деформаций в кристаллической решетке своего вещества.

Попробуй обратиться за помощью к преподавателям

При слишком сильном растяжении или сжатии материал пружины теряет упругие свойства. Такая деформация называется пластической или остаточной.

Формула для расчета частоты колебаний

• Если пружину с закрепленной на ней грузом, подвергнуть продольной упругой деформации, а затем отпустить, она начнет совершать возвратно-поступательные гармонические колебания, в ходе которых перемещение закрепленного на ней груза описывается формулой:
• $x = A cdot cos(omega_0 cdot t + phi)$
• Здесь $A$ – амплитуда колебаний, $phi$ – начальная фаза, $omega_0$ – собственная циклическая частота колебаний пружинного маятника, рассчитываемая как

• $k$ – жесткость пружины,
• $m$ – масса закрепленного на ней тела.

1. Циклическая частота отличается тем, что характеризует не количество полных циклов за единицу времени, а количество «пройденных» колеблющейся по гармоническому закону точкой радиан.
2. Задай вопрос специалистам и получи ответ уже через 15 минут!
3. Период колебаний пружинного маятника вычисляется как
4. $T = 2 cdot pi cdot sqrt$.
5. Найти частоту и циклическую частоту пружинного маятника, период колебаний которого составляет 0,1 с.
6. Частоту можно найти как величину обратную к периоду:
7. Циклическую частоту можно выразить как
8. $omega_0 = 2 cdot pi cdot f$
9. $omega_0 = 2 cdot 3,1415927 cdot 10 approx 62,831854 frac$
10. Ответ: 10 герц и $approx$ 62,831854 радиан в секунду.
11. Так и не нашли ответ на свой вопрос?
12. Просто напиши с чем тебе нужна помощь

Читать также:  Импульсный сварочный аппарат своими руками

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):

В этом соотношении – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

Таким образом, груз некоторой массы , прикрепленный к пружине жесткости , второй конец которой закреплен неподвижно (рис. 2.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором .

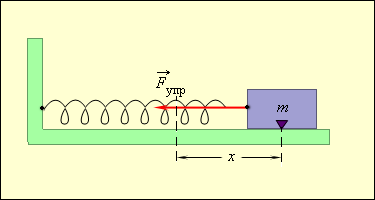Рисунок 2.2.1.

Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона:

откуда

Частота называется собственной частотой колебательной системы.

Период гармонических колебаний груза на пружине равен

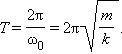При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную

и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае.

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени :

Поэтому второй закон Ньютона для груза на пружине может быть записан в виде

или

(*)

где

Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида

Читать также:  Какая фреза нужна для врезки петель

Уравнение (*) называется уравнением свободных колебаний .

Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период .

Такие параметры колебательного процесса, как амплитуда m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.

• Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то m = , .
• Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость то
• Таким образом, амплитуда m свободных колебаний и его начальная фаза определяются начальными условиями .

Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения:

Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)

где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение.

По аналогии с грузом на пружине можно получить:

Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.